Research

Statistical Mechanics of Materials

We are surrounded by a great variety of materials of astounding complexity, such as metals, inorganic crystals, polymers, colloids, gels, glasses, biological tissue etc. In many of these, entropic effects play a very important role. Many are out of thermodynamic equilibrium, driven by external fields or agents or, like ourselves, examples of “active” matter. Traditional concepts derived, for example, from equilibrium thermodynamics suddenly turn out to be grossly inadequate and new ideas become necessary. Fortunately, theoretical tools and experimental techniques necessary for addressing these questions are being discovered continuously, making this an active field of research. Below we give examples from a few research  projects currently being undertaken in our group.

The thermodynamic origin of solid rigidity

School textbooks tell us that the main difference between a solid and a liquid is the ability of the former to retain its shape. Any attempt at changing the shape of a solid is resisted by an internal elastic stress unless the deformation crosses a limiting value; at which point the solid fails. This naive viewpoint, although of great practical use, is, however, fundamentally incorrect. For example, one can argue that given enough time, atoms in the solid can always rearrange to eliminate stress no matter how much, or how little, the solid is deformed. This result, of course, creates a paradoxical situation. Although the observed limiting failure strengths of solids are of great use for designing engineering structures from bridges to space stations, the meaning of these limiting values becomes unclear. Resolution of this paradox therefore lies at the very core of our understanding of the behaviour of solids under deformation.

Our group, which consists of researchers from the TIFR, Hyderabad, India, The Universities of Dusseldorf and Goettingen, Germany may have the beginnings of an answer [1]. Adapting ideas which were introduced recently to study glasses, we find that every crystalline solid comes in two forms, which are identical in crystal structure but differ in the way they respond to changes of shape. While the first one is rigid and resists changes of shape the second variant always eliminates stress from its bulk and rearranges atoms to conform to shape changes. Further, they are connected by a “first order phase transition” similar to commonly observed liquid-gas or liquid-solid phase changes. When deformed by any amount, howsoever small, the rigid solid goes into a meta-stable state analogous to superheated water. Eventually, this meta-stable state always decays by nucleating bubbles of the stable, stress-free, solid by a process very similar to how bubbles of steam appear in a kettle of boiling water.

This completely novel conceptual viewpoint not only reconciles the paradox but also offers us a way to quantitatively calculate failure strengths of, at least for now, idealised solids. Since decades (1950’s), the standard explanation for deformation in crystalline solids always involved crystal defects namely, dislocations, which represent partially missing or extra crystalline layers. Interactions between dislocations are complex and many-body so that understanding failure of even ideal solids becomes an involved exercise, ultimately requiring empirical inputs. Quite remarkably, our calculation does not involve dislocations and uses standard methods of nucleation theory of first order phase transitions. The calculated failure strength depends on the rate at which the deformation is applied in a very precise way. Such a calculation had till now been intractable. Also, the concept of a dislocation is hard, or rather impossible, to define in amorphous matter, which lacks well defined crystal layers. We believe that our approach, which does not use dislocations may have much more general applicability in such solids. Finally, our work unifies two seemingly disparate fields namely, the study of deformation of materials and that of phase transitions.

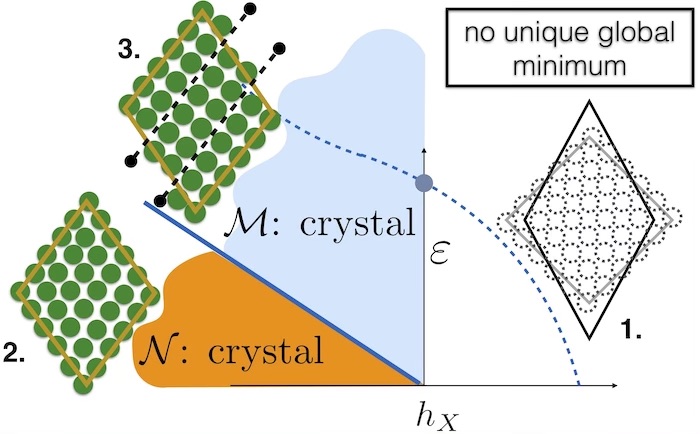
Fig 1. The main result from our research is summarised in this figure. We show that there is a first order phase transition between two kinds of crystals – the “normal” or N crystal (2) and a “Meissner” crystal (3) which eliminates stress when the original lattice (1) is deformed. The equilibrium N-M transition cannot be observed, however the dynamical consequence of this transition is the existence of a limiting value of strain where the metastable N crystal decays to the stable M phase.

[1] “On the existence of  thermodynamically stable rigid solids” P. Nath, S. Ganguly, J. Horbach, P. Sollich, S. Karmakar and S. Sengupta, PNAS 115 E4322-E4329 (2018).

Further reading: A relevant blog-post

Ligand binding and allostery in proteins

Drugs are typically designed by first identifying a protein which is relevant to the progression of a specific disease and then synthesising small molecules which interfere with the functioning of this protein by binding to it. The binding of proteins to small molecules is also important for many biochemical processes essential to life. It is therefore not surprising that a great amount of time and effort is spent in determining the processes by which ligands bind to proteins. Apart from the primary binding site in proteins there also exists secondary sites which can influence the primary binding reaction either positively or negatively. Such control mechanisms, known as allostery, is crucial to the functioning of many enzymes and other protein based bio-chemical machinery in the cell.

In recent times, in-silico experiments, using all-atom molecular modelling, has started to provide crucial inputs to our knowledge of the working of proteins and their binding activity. Even so, discovery of binding pathways of small molecules both at the primary binding site, as well as sites for allosteric control, is time consuming and often fortuitous.

In our group we are trying to set up a novel framework [2] within which critical conformational changes likely to occur during binding are quantified from statistical analysis of configurations of proteins in their apo, or inactive form, greatly simplifying identification of binding processes. We show that possible primary and secondary binding pathways can be discovered from short simulations of the apo-protein without waiting for an actual binding event to occur. We use a projection formalism, introduced earlier to study deformation in solids, to analyse local atomic displacements into two mutually orthogonal subspaces—those which are “affine” i.e. expressible as a homogeneous deformation of the native structure, and those which are not. The susceptibility to non-affine displacements among the various residues in the apo- protein is then shown to correlate with typical binding pathways and sites crucial for allosteric modifications.

Fig. 2 An animation showing an allosteric correlation between two sites in the protein T4 Lysozyme, which has been captured in our analysis. The hydrogen bond breaking in one site (yellow) is correlated with the opening (untwisting) of a helix at another (black). 

[2]”On identifying collective displacements in apo- proteins that reveal eventual binding pathways” Dheeraj Dube, Navjeet Ahalawat, Himanshu Khandelia, Jagannath Mondal and Surajit Sengupta, PLoS Comput Biol 15(1): e1006665 (2019).

Translationally invariant colloidal crystal templates

Crystals made out of artificial colloids, eg, small spheres of latex or silica suspended in water, are valuable as easily accessible tools for the study of materials behaviour as well as, in their own right, as photonic crystals. The length scales – of a few microns to tens of nanometers and time scales of the order of seconds make the extremely suitable for study using light microscopes and other standard laboratory apparatus. Colloidal crystals may occur in a variety of forms with their structure being amenable to modification by chemical and physical means. The former is accomplished by tuning interactions by creating special surface patches or attaching DNA tethers and the latter using etched templates or laser traps. While chemical modification is permanent – the structure is fixed once the interactions are, static laser traps and templates break translational invariance and destroys some or all phonon modes making them massive.

Is it possible to arrange colloidal particles interacting with any given potential into any desired crystal structure without affecting translational invariance and preserving all the phonon modes? It is possible to produce structures which are metastable or even completely unstable and study their properties? Is it possible to switch from one structure to another at the flip of a switch?

In our group, we have proposed exactly such an experiment and if implemented should usher in a completely new generation of optical trapping of colloids.

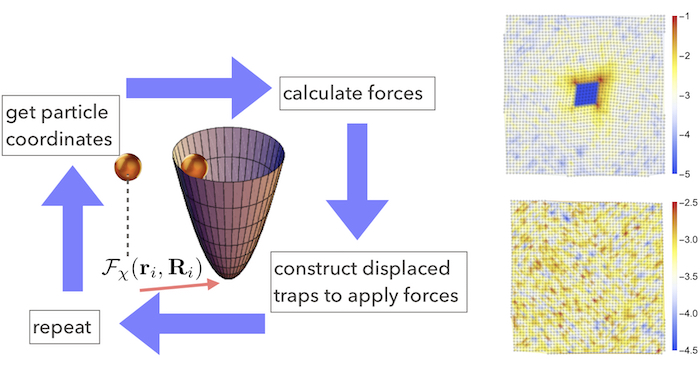
Fig. 3 A schematic showing the proposed implementation of dynamical, feedback controlled laser traps (left). Particle configurations from a stable square lattice formed of colloids interacting by an isotropic potential in two dimensions (right). 

[3] “Translationally invariant colloidal crystal templates”, Pankaj Popli, Saswati Ganguly and Surajit Sengupta, Soft Matter, 14, 104 (2018).

Active segregation of chromosomes

Living matter is always in a non-equilibrium state. It is also “active” in the sense that energy is continuously being produced and dissipated locally and not from the boundaries. Active matter can be driven into interesting non-uniform states. We have shown that such an active driving, a consequence of gene transcription processes is at the heart of chromosome organisation in the nucleus of eukaryotic cells. It is known that chromosomes containing a large number of expressed genes occupy the centre of the nucleus whereas those which are “switched off” lie in the periphery. Errors in this organisation can lead to diseases such as progeria. The reason for this was not understood. We have now shown that this results from a local “active temperature” arising from differential biological activity [4].

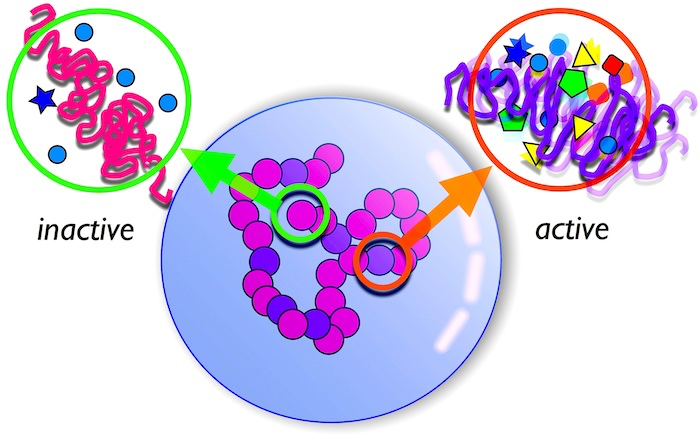
Fig. 4 A schematic showing segregation and organisation of a chromosome based on the level of activity at the various locations along its length. Active regions occupy interior spaces within the nucleus. 

[4] N. Ganai, S. Sengupta, G. I. Menon, Nucleic Acids Research, DOI: 10.1093/nar/gkt1417 (2014).