Research
The research interest in my group has two broad directions. First, we use statistical mechanics tools and concepts for the physics of nonequilibrium and glassy systems. Specifically, we want to develop a theoretical framework for the mechanism governing the glassy dynamics. Second, we apply various physics principles to understand the properties of diverse biological systems.
I will briefly describe some of the problems we are currently interested in our group.
Glassy dynamics and glass transition
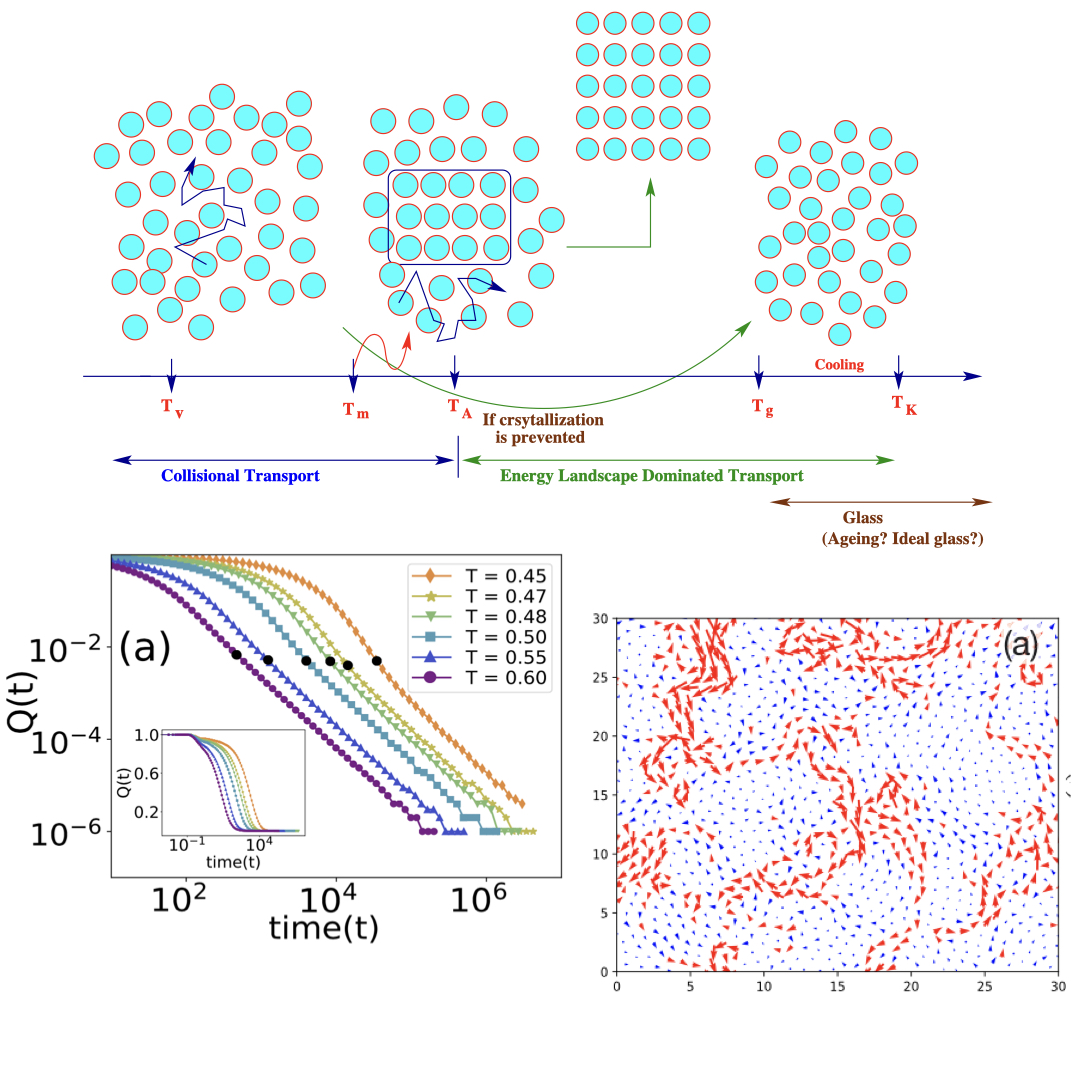
Glassy dynamics refers to the extreme dynamic slow down without an apparent phase transition. When cooled, a liquid can become a crystal when the temperature goes below the crystallization temperature. However, crystallization is a time-consuming process: first, a tiny volume of the crystalline phase nucleates, and if its volume is large enough, it grows and spans the entire system. Both the nucleation and the growth take time. What happens if you do not allow enough time? The relaxation time and viscosity of the liquid continue to grow, and it becomes impossible to keep the system equilibrated after some time; this is known as the glass transition. Note that no thermodynamic phase transition is associated with the glass transition, yet the material becomes solid for all practical purposes.
The nature of glass and glass transition remains one of the deepest and most interesting unsolved problem in solid state theory [P. W. Anderson, Science 267, 1615 (1995)]. Apart from its theoretical importance, glassiness is crucial in several fields, such as econophysics, earthquakes, industry, dynamics in biological systems, etc. However, the mechanism behind the glassy dynamics remains unclear despite the presence of many theories in the field. In this direction, we want to develop a theoretical framework to understand the glassy dynamics and the nature of glass transition.

Fluctuation-dominated phase ordering
Fluctuation-dominated phase ordering (FDPO) refers to the coexistence of macroscopic fluctuations with long-range order. Consider a system where two phases coexist. The boundary separating the two phases is often sharp (of the order of a few molecular diameters). By contrast, in systems exhibiting FDPO, this boundary can be anomalously broad and scales with the system size. There exist several such systems. Examples include particles on a fluctuating surface, active particles, vibrating rods, freely cooling granular colliding systems, actin clusters on the cell surface, etc. They show several usual properties, such as a broad distribution of the order parameter in the steady states, giant fluctuations, violation of Porod’s law, and a cusp singularity in the scaled two-point correlation function. The field is still in its infancy, and many questions remain unexplored. What are the effects of FDPO on the static and dynamic properties of the system? What are the main criteria for the existence of FDPO? What is the nature of the critical point in systems with FDPO?
Statistical physics of model systems
In physics, we want to understand the underlying fundamental principles governing the properties of various systems at different scales. One powerful approach to understanding complex phenomena and systems is to develop simple models to illustrate specific mechanisms. We often take this approach and define spin models or simple one-dimensional systems with distinct rules to allow detailed analytical and numerical solutions. For example, we have developed various models and are working on them to understand the role of spatial heterogeneity, long-range interactions, dynamical or kinetic constraints, initial conditions, etc. Once we know the behavior of these simple systems, we can use various mapping and different concepts of statistical physics, such as the universality class, and better comprehend the properties of the actual systems of our interest.

The glassy dynamics in biological systems
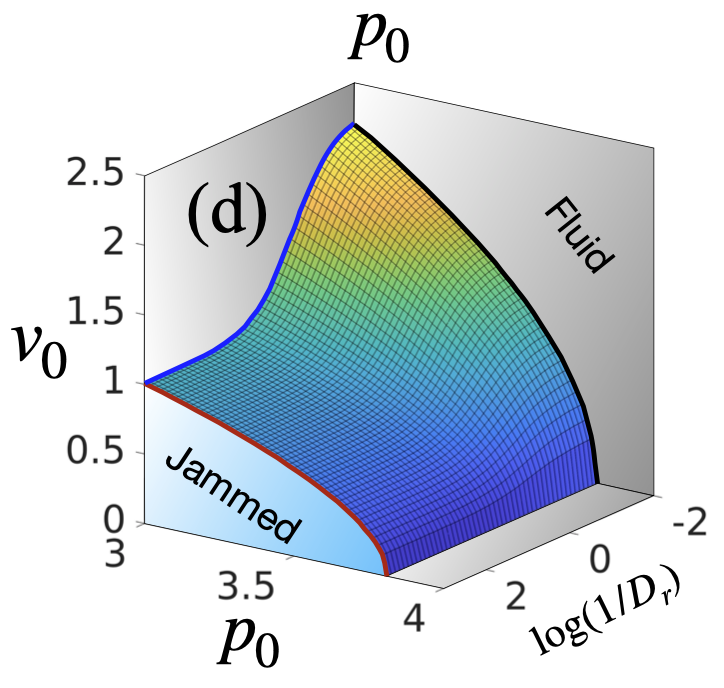
Many experiments in the last decades have shown that glassy dynamics is crucial for various biological processes, such as morphogenesis, wound healing, and cancer metastasis. Although simulations have provided critical insights, not much analytical theory exists due to the complexity of the systems. We are developing such theoretical frameworks to study the glassy dynamics in biological systems. Biological systems are active by nature. In two distinct directions, we are exploring the effect of activity on the glassy dynamics and studying the glassy properties of confluent cellular systems where the cells entirely cover the space.
We are also formulating a novel approach via the elastoplastic models to investigate the glassy dynamics in active systems. We combine analytical theory with simulations and then compare the theoretical predictions in experiments.
Static and dynamic properties of confluent cell monolayer
The static and dynamic properties of cells in a monolayer are crucial for several biologically significant processes, such as embryogenesis, wound healing, cancer progression, etc. However, a comprehensive theoretical framework to understand cellular properties is lacking.
Using physical models of epithelial monolayers, we have developed various tools and techniques to address the physical processes at the early stage of cancer. We are addressing several aspects of the problem: Are there any static or dynamic features of a cluster of cells with different properties? What are the physical consequences of confluency (where cells entirely cover the space)? How to study their dynamical properties?
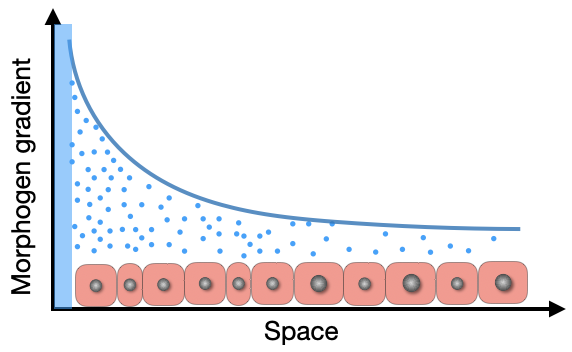
Symmetry breaking and pattern formation in biology
Pattern formation, symmetry breaking, or morphogenesis refers to the emergence of patterns starting from a single cell; it is essential for any higher form of life. Most theoretical studies of pattern formation represent cells as point particles. However, cell shape has crucial implications. The systems of our interest are, for example, embryogenesis, wing-disk development, and organ formation in general.
These systems are confluent, where there is no intercellular gap. Theoretical frameworks for morphogenesis require three main ingredients: a morphogen gradient, cellular dynamics, and functions such as division, apoptosis, and differentiation. The gradient formation is relatively well understood. We have been developing simplified descriptions for the other two aspects. We now know that the dynamics is glassy, and we are formulating analytical theories to describe the dynamics in confluent systems.
Analytical theory for functions is more challenging. We are taking a slightly indirect route, using the `mechanistic’ point of view. The idea is similar to statistical physics, where we express the macroscopic observables via various parameters, such as temperature and density, ignoring the detailed particle positions. Many past works have shown that such a possibility might exist using cell shape as a parameter. We have developed an analytical theory for cell shape and are now applying the theory to the functions.
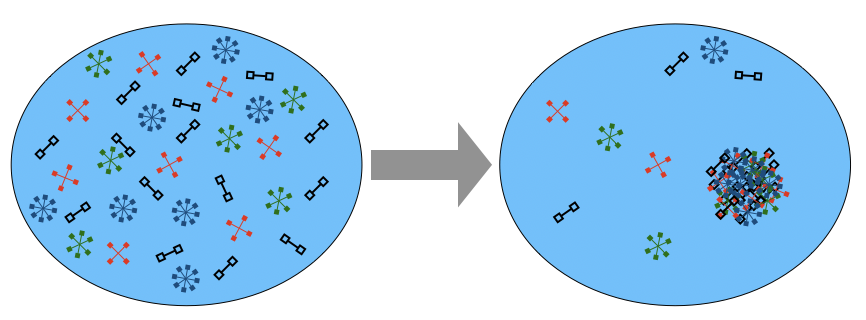
Liquid-Liquid Phase Separation and protein aggregation
Cells organize different biochemical reactions via compartmentalization. Some of the compartments are membrane-bound, and others are non-membrane-bound. In 2009, Brangwynne and others showed that the non-membrane-bound compartments, the biomolecular condensates (BMCs), form via liquid-liquid phase separation (LLPS). BMCs are crucial for both health and disease. They can spatially localize biochemical processes and can have different regulatory roles. But, aberrant protein self-assembly can be detrimental to health. A quantitative understanding of the phase separation process in the intracellular complex environment is nontrivial due to the involvement of many components, the intrinsically disordered nature of the proteins, and a lack of complete knowledge of their properties. A detailed understanding of intracellular phase separation is in its infancy, and we are addressing some of these aspects.
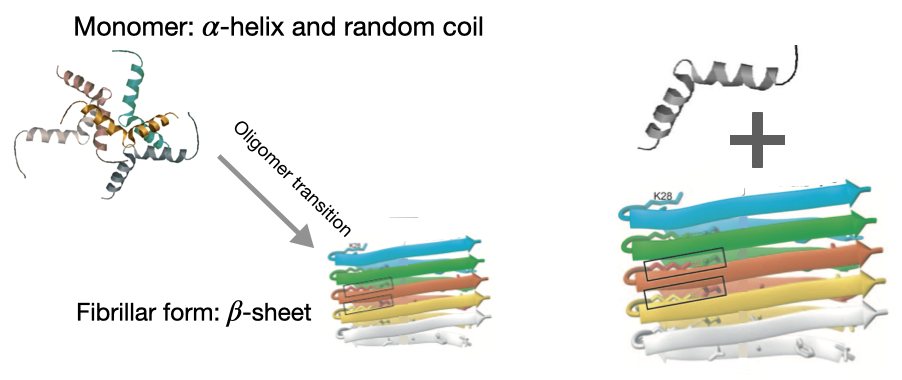
We are also investigating the mechanisms of aberrant protein aggregation; they lead to various neurodegenerative diseases such as Alzheimer’s or Huntington’s disease, type II diabetes, etc. We want to understand both the fundamental mechanism and the regulatory aspects of the problem. One crucial step is the protein conformation change that initiates this process. We are addressing the process at varying lengths and time scales.