Granular Systems and Lattice Gases


As finite sized rigid particles are brought together by increasing their density or by compression, they undergo sharp transitions into globally rigid structures, a phenomenon known as `jamming'. Such systems do not form periodic spatial patterns associated with crystalline solids, instead they display amorphous rigidity.


Jamming of Soft Particles

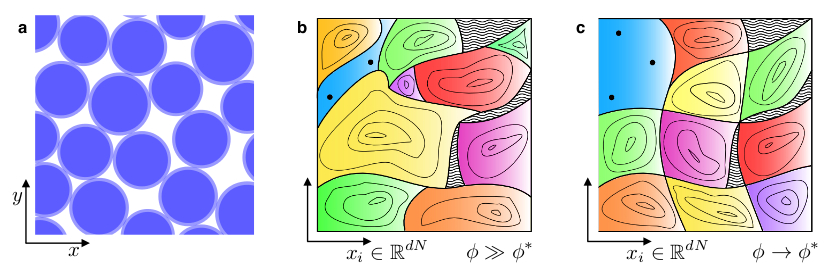FIG 1: (a) Snapshot of a jammed packing of disks with a hard core (dark shaded regions) plus soft repulsive corona (light shaded regions). (b)-(c) Illustration of the energy landscape for jammed packings, showing several basins of attraction (colored). As the system approaches unjamming ($\phi \to \phi^*$), these basins become similar in size.

Jamming transitions are ubiquitous in nature. They affect systems ranging from the mesoscopic lengthscales to macroscopic particulate matter. It frequently occurs in materials of practical importance, such as foams, colloids, grains and even biological tissues, when these systems become rigid in the absence of thermal fluctuations. Decompressing such solids to the point where mechanical equilibrium can no longer be achieved leads to `unjamming'. At present, both the exact nature of the ensemble of jammed states and the unjamming transition remain unclear. A key assumption underlying a statistical description of granular matter, proposed by Edwards, is that all jammed packings are equally likely. The logarithm of the number of such packings was postulated to play the same role as entropy does in Gibbs' statistical-mechanical description of the thermodynamic properties of equilibrium systems. To test the entropy of such systems, it is advantageous to study soft disks near unjamming, where in contrast to systems with hard constraints, it is possible to explicitly compute the number of jammed packings. The volume of the basin of attraction $v_i$ of each stable packing (see Fig. 1), defines a probability $p_i \propto v_i$ of finding this basin. We numerically computed these volumes for $64$ hard disks with soft outer shells at different packing fractions $\phi$. The number of jammed states is, explicitly, $\Omega (\phi) = V_J (\phi)/\langle v \rangle (\phi)$, where $V_J (\phi)$ is the total available phase space volume at a given $\phi$, and $\langle v \rangle (\phi)$ is the average basin volume. Equiprobability can be checked by comparing the granular (Boltzmann) entropy $S_B = \ln \Omega - \ln {N !}$, which counts all packings with the same weight, with the Gibbs entropy $S_G = - \sum_i^{\Omega} p_i \ln p_i - \ln {N !}$. These entropies satisfy $S_G \leq S_B$, being equal when all $p_i$ are equal. We found that remarkably, the Gibbs and the granular entropy approach equality very close to unjamming, indicating that the Edwards formalism for hard disks might hold true.

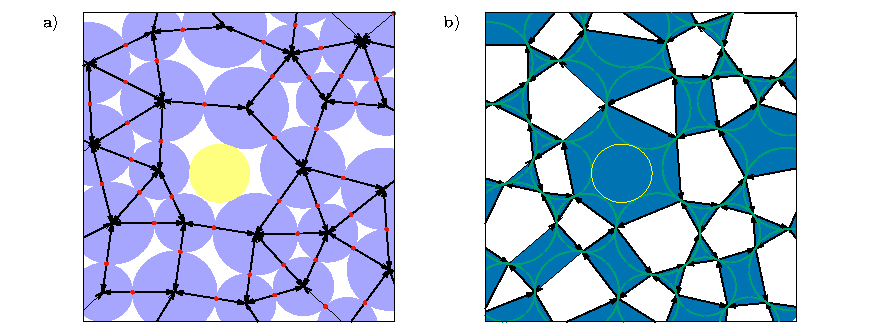FIG 2: a) A section of a jammed packing of bidispersed frictionless disks, along with the contact network (black arows). b) The same section with the polygonal representation that cyclically connects the contacts within each grain. The rattlers (disks with no contacts) are shown in yellow.

Several studies have shown that the unjamming transition in systems of soft particles is characterized by power-law scaling of many physical properties. We used a polygonal partitioning of space based on inter-grain contacts (see Fig. 2) and identified a global order parameter, the fraction of covered area $A_G$, that can serve as a substitute for the packing fraction (and avoids some of the problems associated with it). We found that the transition occurs at $A_G^{*} = 0.446(1)$ and determined new critical exponents using this order parameter. We used this to study the underlying geometric disorder and found that a finite fraction of order $\Psi_O^* = 0.369(1)$ persists as the transition is approached. We developed a scaling theory by uniquely assigning local areas to each contact. These local order parameters exhibit divergences in their distribution as unjamming is approached, with scaling forms being predictable by a mean-field approach that includes three-body correlations. These results agree remarkably well with numerical simulations, even predicting the observed power law scaling of global quantities. This represents the first microscopic derivation (albeit mean-field) of the power-law exponents in this well-studied system, highlighting differences between standard critical phenomena and the jamming transition.



Lattice Gas Mixtures

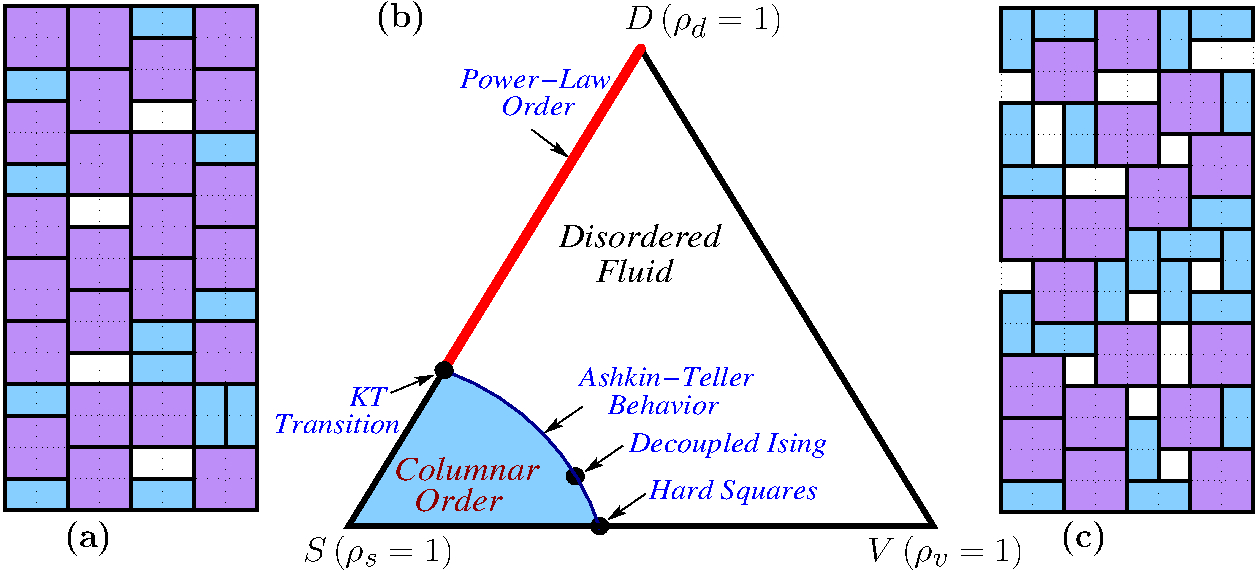FIG 3: (a) Part of a high-density columnar ordered configuration of $2 \times 1$ dimers and $2 \times 2$ hard squares on the square-lattice. (b) Schematic phase diagram. $\rho_s,\rho_d$, and $\rho_v$ are the densities of squares, dimers, and vacancies respectively, with $\rho_s + \rho_d +\rho_v =1$. (c) Part of a lower density configuration displaying disordered fluid behaviour.

Lattice gas models, in which particles are constrained to be on the sites of a lattice and interact via extended hard-cores, serve as the easiest models of complex physical systems such as simple fluids, structural glasses and granular materials. Simple lattice-gas models, such as $2\times1$ dimers and $2\times2$ hard-squares on the square lattice, have long been of special interest. In the hard square lattice gas the crystalline state has a sliding instability that leads to long-range columnar (stripe) order in the high-density phase. We showed that critical exponents of the transition to columnar order in a more general mixture of $2 \times 1$ dimers and $2 \times 2$ hard-squares on the square lattice (Fig 3 a) depends on the composition of the mixture as predicted by the theory of Ashkin-Teller criticality, including in the hard-square limit. This result settled the question regarding the nature of the transition in the hard-square lattice gas, which was the subject of some controversy. Ashkin-Teller transitions are interesting exceptions to universality, and this provided the first example of a polydisperse system whose critical properties depend on composition.