Correlations in Disordered Systems


Correlated random events play a prominent role in the physics of disordered systems. The distributions of, and gaps between the extreme values of such events finds applications in fields across all sciences, and is the subject of Extreme Value Statistics (EVS). Studying such distributions in the context of physically relevant models provides a fertile avenue for future research.


Random Field Ising Models

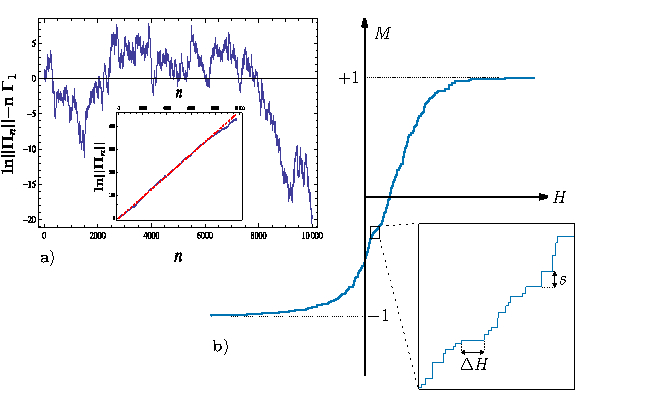FIG 4: a) Fluctuations of the product $\Pi_n=T_n\cdots T_1$ of transfer matrices of the RFIM. The inset shows the growth in $\ln||\Pi_N||$. b) The increase in magnetization per site $M$ in the RFIM at zero temperature in a monotonically increasing external field $H$. The jumps of size $s$ correspond to avalanches and are separated by gaps $\Delta H$ in external field increments.

Random Field Ising Models (RFIMs) have been paradigmatic systems to study disordered materials, and provide a natural system where correlated exteme values arise. We have studied the products of transfer matrices $T_n$ associated with one dimensional RFIMs. Most of the physics is captured by the extreme eigenvalue, describing the growth rate of the Random Matrix Product (RMP) $\Pi_N=T_N\cdots T_2T_1$ through the Lyapunov exponent $\Gamma_1=\lim_{N\to\infty}\ln||\Pi_N||/N$. This is closely related to quantum localization in one dimension and even to systems that display anamalous diffusion. Although $\Gamma_1$ describes the mean free energy of the RFIM, the fluctuations of the RMP (Fig. 4 a) also play an important role, particularly in the context of localization, where they dominate several physical quantities. We analytically characterised the fluctuations in a particular sequence of RMPs and showed that $\Gamma_1$ is in some cases (such as near a delocalization transition) insufficient and the second moments provide the dominant length scales at low energies. Another aspect of disordered systems that RFIMs can describe is `crackling noise', their characteristic intermittent response when subjected to an external drive, caused by internal avalanches. Recently, we studied the statistics of gaps ($\Delta H$ ) between successive avalanches triggered by a monotonically increasing external field $H$, in one dimensional RFIMs. An important distinguishing feature of marginally stable solids is a non-zero exponent $\theta$ characterizing such gaps, defined as $P~( \Delta H ~) \sim \Delta H^{\theta}$ as $\Delta H \to 0$. By mapping the sequence of avalanches in the ferromagnetic system to a non-homogeneous Poisson process, we analytically computed the distribution of gaps and showed that $\theta = 0$. In contrast, we found through numerical simulations that a long-range antiferromagnetic RFIM displays a $\theta \approx 0.95(5)$. This provided one of the few microscopic Hamiltonians without disorder in the interactions that displays such a behaviour, in contrast to the well-known spin glass models.



Branching Brownian Motion

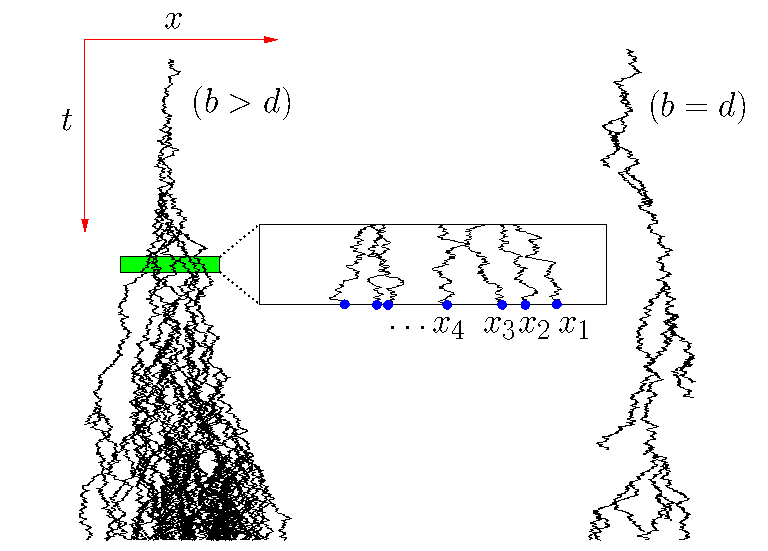FIG 5: A realization of the dynamics of branching Brownian motion with birth rate $b$ and rate of death $d$ (left) in the supercritical regime ($b > d$) and (right) in the critical regime ($b = d$). We studied the order statistics and spatial extent of this process.

Another interesting system involving correlated random processes is the branching Brownian motion (BBM), which is a prototypical model of evolution and finds many applications in physics and biology. In BBM, particles split into two independent offsprings with a rate $b$, die with rate $d$ or diffuse (see Fig. 5). The existing particles at time $t$ are correlated through their common genealogies. Depending on the relative rates of birth and death, the process is either explosive ($b > d$), critical ($b = d$), or eventually dies ($b < d$). In the $b > d$ regime the cumulative distribution of the rightmost particle satisfies a non-linear FKPP equation and the extremal particles travel outwards with a finite velocity. In the $b \le d$ regime, the gap distributions become stationary. We derived exact results for this stationary joint distribution of these extreme values, and we derived an exact expression for spatial extent of BBM, in the $b \le d$ regime. Our results demonstrated that the correlations between the extreme values persist even in the stationary state, a fact that has important implications in spin glass theory. We showed analytically that the particles display an interesting clustering, in which there are two length scales in the system, the length scale of the gap between the particles which tends to a constant at large times and the length scale of the fluctuations which grows as $\sqrt{t}$.