Dynamics of Constrained Systems


Systems with a macroscopic number of constraints often display interesting thermodynamic properties such as infinite-order phase transitions or very sharp first-order phase transitions. Several issues can arise when dynamics are introduced, which depend on the microscopic details and the energetics of near-excited states. The dynamics of several constrained systems slows down dramatically at low temperature, and often display dynamical heterogeneity as seen in supercooled liquids. Although several disparate systems display characteristically `glassy' behaviour, a comprehensive theory explaining the microscopic origins of glass transitions is still missing.

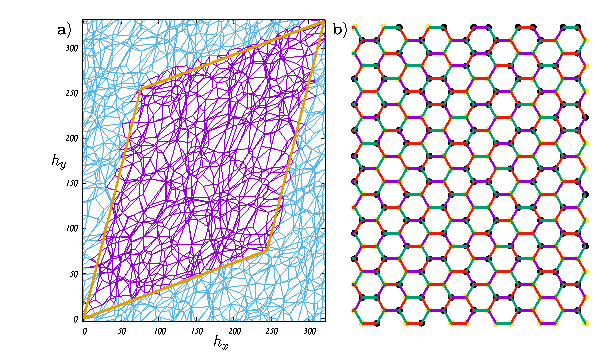FIG 6: a) The force tiling associated with a flowing dense suspension of $2000$ soft disks. The bonds correspond to the internal forces, with larger polygons representing grains with higher stress. The blue regions represent periodic copies of the system. b) A valid configuration of the three-coloring model, along with the chirality (Ising) variables at each site.

Stress Transmission in Flowing Suspensions

Dense suspensions of grains in a fluid display shear thickening (an increase in viscosity $\eta = \sigma/\dot{\gamma}$) as the confining stress ($\sigma$) or strain rate ($\dot{\gamma}$) are increased. The steady state flow of such suspensions is governed by the microscopic constraints of force and torque balance. At a critical, density dependent $\sigma$, the viscosity jumps abruptly with increasing $\dot{\gamma}$, a phenomenon termed Discontinuous Shear Thickening (DST). This has been attributed to the frictionless lubricated layers between grains giving way to frictional contacts as they are pushed together at large $\dot{\gamma}$. The constraints on the stress tensor along with the non-isotropic fabric of the underlying material leads to forces being primarily carried by a sparse, tenuous network of contacts known as ``force chains". DST is reminiscent of classical phase transitions, and a key question is how interactions between the microscopic constituents give rise to a macroscopic transition. A confluence of ideas from the granular and fluid dynamics communities has led to new understanding and questions regarding the flow of dense suspensions. Recently, we developed a framework for stress transmission in such materials that respects vector force balance at the microscopic level. By mapping this problem onto the spectral properties of the graph Laplacian of the underlying contact network, we showed that this leads to spatial localization of forces. This allowed us to assign the hydrodynamic drag which acts as a body force on each particle to the underlying contact forces in the system. We performed a quantitative analysis of the collective evolution of the contact-force network accompanying the DST transition. Our study, based on a dual space representation of the stresses (known as force tiles, see Fig. 6 a) demonstrated clear changes in the distribution of microscopic variables, and led to the identification of an `order parameter' characterizing DST.



Glass Transitions in Constrained Spin Models

Exactly soluble models with hard constraints are particularly appealing in terms of their theoretical tractability. An interesting example is the problem of coloring the edges of a hexagonal lattice with three colors such that no site has a repeated color (see Fig. 6 b). In this case, the entropy per site $q = 1.20872...$, can be computed exactly. Each valid state can be exactly mapped onto a folded configuration of a triangular lattice and is interesting in the context of crumpling transitions that are observed in nature. When energetics are introduced through chirality (Ising) variables, this provides one of the simplest models of glassy behavior in a Hamiltonian model without quenched disorder. In order to maneuver within the phase space of allowed states, non-local loop dynamics need to be introduced. Monte Carlo studies have shown that time scales obey a Vogel-Fulcher law as the temperature approaches a dynamical transition temperature, mimicking fragile structural glasses. We have studied variations of the three-color model with short-range interactions using a transfer matrix analysis that is able to extract the free energy of a $L \times \infty$ lattice in a numerically exact manner. By imposing boundary conditions drawn from an equilibrated bath we are testing entropy-driven cavity melting in this model and the corresponding folded membrane.