Research
This webpage gives an overview of my recent and current research in statistical physics, both in and out of equilibrium. I am interested in systems that reach a balance between large fluctuations and order; between coalescence and breaking; and between short-range repulsion and long-range attraction coming from shared histories.
Fluctuation-dominated States are characterized by giant fluctuations. The hallmarks of fluctuation-dominated phase ordering (FDPO) are a broad distribution of the order parameter, and a cusp singularity of the scaled correlation function. Much more intense clustering can occur if hard-core interactions between particles are absent. This results in fluctuation-dominated clustering (FDC), where the cusp is replaced by a stronger singularity, namely a divergence, and there are strong signatures of intermittency.
Fluctuation-dominated phases occur in many types of systems: passive particles carried by a compressible fluid, lipid clustering on cell membranes, coarsening in the Vicsek model of flocking, active nematics, vibrated rods and inelastically colliding particles. Particles sliding on a fluctuating surface show FDPO if there are hard core interactions, and FDC if there are none. FDPO has been established analytically on the critical line of a 1D Ising model with long-range interactions. FDPO and FDC provide a framework to discuss diverse systems which display fluctuation-dominated phases.
The figure shows space-time plots of passive sliding particles driven by interfaces. Particles cluster laterally to different extents depending on relative directions of particle sliding and motion of the fluctuating interface, which differs from panel to panel. Shared histories lead to particles aggregating intermittently, forming clusters which make and break. The system exhibits FDC. Sliding particles cluster very strongly when sliding and interface motion are in consonance (left panel); they cluster less strongly when the interface does not move as a whole (middle panel); and even less strongly when the interface motion is opposite to particle sliding.
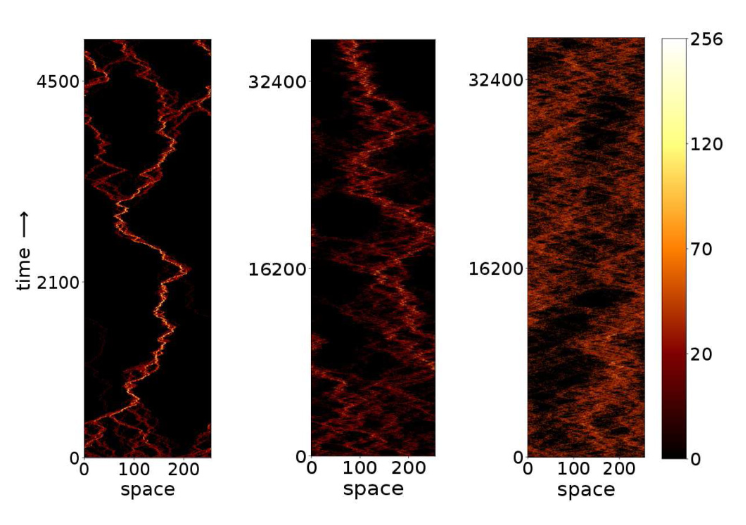
Left panel: Along sliding direction. Middle panel: Stationary. Right panel: Against sliding direction.
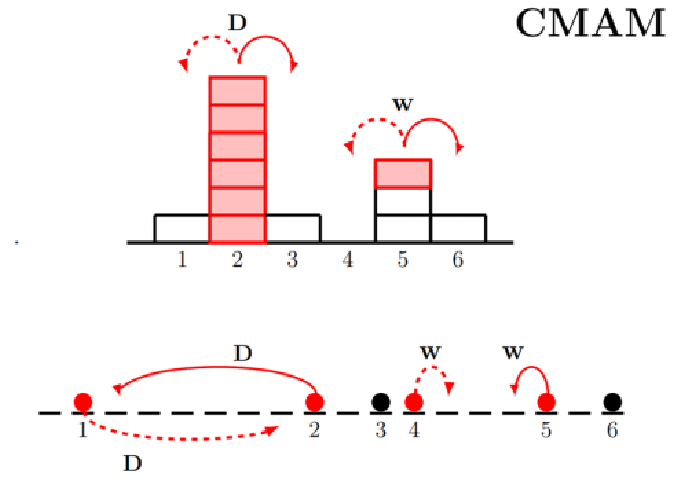
Aggregation-Fragmentation Dynamics can lead to a state with a condensate or macroscopically large aggregate, via a phase transition. The figure shows a model which exhibits this. It involves the competition between diffusion cum coalescence on the one hand (at rate D) and chipping, or breaking a single particle on the other (at rate w). During the approach to the steady state, local condensates form within a coarsening length scale, which grows in time; the distribution of condensate masses exhibits scaling, and this implies anomalously large fluctuations: the standard deviation is as large as the mean. Remarkably, the state of the system during coarsening is governed not by the steady state but rather a pre-asymptotic state — a breakdown of the familiar local steady state hypothesis.
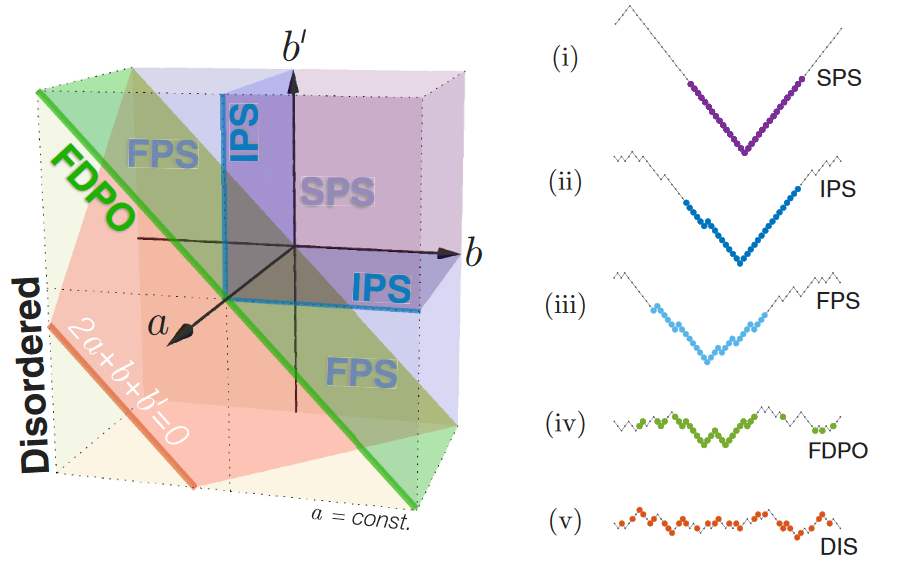
Interesting phases are exhibited by Coupled Driven Systems in which the local density of each species (particles, and slopes of a fluctuating interface) influences the dynamics of the other. There are interesting phase transitions from a disordered state to several types of ordered states with phase separation (see the accompanying figure). These ordered phases show complete segregation of particles and holes, but their macroscopic slopes differ. Strong phase separation (SPS) refers to a phase in which the particle current is practically zero. In the IPS phase, there is an infinitesimal current of order inverse system size, while there is a finite current in the FPS phase. On the boundary between ordered and disordered phases, the system exhibits FDPO. In the disordered phase, the steady state was found exactly in a subspace of parameters and shown to be of product measure form. This was shown by invoking a new balance principle, which generalizes the principle of detailed balance and the condition of pairwise balance. In the disordered phase, the dynamics involves coupled-species propagating modes. These can be grouped into universality classes, with distinct dynamical exponents. As parameters are varied, these coupled modes develop instabilities, which herald phase transitions to the ordered states discussed above.